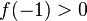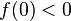حل معادلات درجهٔ دوم
همانند حل معادلات درجهٔ اول برای پیدا کردن نقاط تقاطع معادله با محور xها صورت کلی معادلات درجه دوم را نوشته و عرض آن ( y ) را برابر صفر قرار می دهیم، پس داریم :
با حل معادله ی فوق مقادیر x را بدست می آوریم، توجه کنید که a برابر با صفر نمیتواند باشد چون در این صورت معادله از نوع درجه اول میشود. پس با شرط a≠0 معادله را حل می کنیم :
اگر ضرب چند عبارت برابر با صفر باشد پس حداقل یکی از آنها صفر است، از آنجا که a بنا بر شرط اولیه نمیتواند صفر باشد پس عبارت داخل پرانتر صفر میباشد، پس داریم :
برای حل معادله آن را تبدیل به مربع کامل می کنیم :
حالا از طرفین معادله جذر می گیریم تا مقدار x را درآوریم :
در نتیجه معادله دارای 2 ریشهٔ زیر میباشد:
معمولاً عبارترا برابر با حرف دلتای بزرگ
نمایش میدهند، دلتا در ریاضیات نماد فاصله یا تغییرات است.
طبق قضیهٔ تثلیث دلتا میتواند مقادیر زیر را اختیار کند :
1 -که در آن صورت فاصلهٔ بین دو ریشه مثبت است، پس معادله دو ریشهٔ مختلف دارد
2 -که در آن صورت فاصلهٔ بین دو ریشه صفر است، پس هر دو جواب معادله یکی هستند و معادله اصطلاحاً ریشهٔ مضاعف دارد
3 -که در آن صورت فاصلهٔ بین دو ریشه عددی منفی است و همانطور که می دانید فاصله عددی منفی نمیتواند باشد، از سوی دیگر از آنجا که
در زیر رادیکالی با فرجهٔ زوج است تنها میتواند مقادیر بزرگتر یا مساوی صفر را اختیار کند.


 میباشد که در آن
میباشد که در آن  عرض اصلی ،
عرض اصلی ، 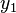 عرض اولیه ، m شیب نمودار و x متغیر طول نمودار میباشد، همچنین در اکثر منابع شکل اصلی معادلات درجهٔ اول به صورت
عرض اولیه ، m شیب نمودار و x متغیر طول نمودار میباشد، همچنین در اکثر منابع شکل اصلی معادلات درجهٔ اول به صورت 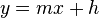 نمایش داده میشود که در آن h همان عرض اولیه است که به اختصار از کلمهٔ height استفاده میشود
نمایش داده میشود که در آن h همان عرض اولیه است که به اختصار از کلمهٔ height استفاده میشود

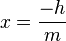



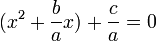
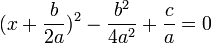
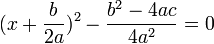

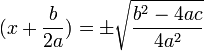

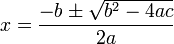
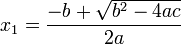
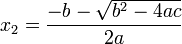
 است.
است.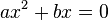
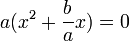


 خواهد بود
خواهد بود
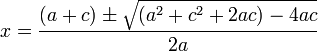

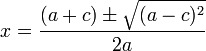
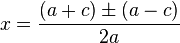


 خواهد بود
خواهد بود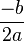 خواهد بود.
خواهد بود.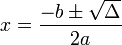

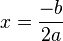 نکته : همانطور که می دانید در صورتی که م
نکته : همانطور که می دانید در صورتی که م

 و
و  ، جواب از مثبت به منفی یا از منفی به مثبت تغییر علامت داد، آن گاه حداقل یک جواب بین
، جواب از مثبت به منفی یا از منفی به مثبت تغییر علامت داد، آن گاه حداقل یک جواب بین 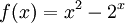 (
این معادله از معادلات بسیار معروفی است که با این روش ریشهٔ دیگر آن بین
(0,-1) حدس زده میشود ) است و می دانیم که نمودار این تابع در بازهٔ [0,-1]
پیوسته میباشد، در این صورت اگر معادله تغییر علامت دهد ( از مثبت، منفی
یا از منفی
(
این معادله از معادلات بسیار معروفی است که با این روش ریشهٔ دیگر آن بین
(0,-1) حدس زده میشود ) است و می دانیم که نمودار این تابع در بازهٔ [0,-1]
پیوسته میباشد، در این صورت اگر معادله تغییر علامت دهد ( از مثبت، منفی
یا از منفی