
اخبار فناوری و شبکه
تازه های شبکه و IT
اخبار فناوری و شبکه
تازه های شبکه و ITنظرسنجی
جدیدترین یادداشتها
همه- جدیدترین آسیب پذیری های امنیتی 2023 در مایکروسافت
- ایجاد و پیکربندی DNS Zone در ویندوز سرور 2022
- سیستم مدیریت امنیت اطلاعات (ISMS) چیست؟
- آموزش کار با نرم افزار PyCharm
- ۱۰ عدد شگفتانگیز دنیای ریاضیات
- معرفی برترین سایت های آموزش زبان برنامه نویسی پایتون
- راهنمای جامع ارتقای رم لپ تاپ (+ آموزش تصویری)
- فروش حضوری محصولات مای نوکیا
- نقد و بررسی مشخصات سامسونگ galaxy J6 و galaxy J6 plus
- بهترین گوشی های موبایل پیشنهادی بر اساس قیمت (ویژه نوروز 1398)
بایگانی
- مرداد 1402 3
- فروردین 1398 16
- دی 1397 5
- آذر 1397 8
- تیر 1397 1
- خرداد 1397 10
- اردیبهشت 1397 5
- فروردین 1397 1
- آذر 1396 13
- خرداد 1396 5
- اردیبهشت 1396 4
- بهمن 1395 3
- اردیبهشت 1395 2
- بهمن 1394 17
- دی 1394 67
- آذر 1394 25
- آبان 1394 15
- مهر 1394 30
- شهریور 1394 16
- مرداد 1394 47
- تیر 1394 6
- خرداد 1394 12
- اردیبهشت 1394 115
- فروردین 1394 13
- اسفند 1393 5
- بهمن 1393 6
- دی 1393 2
- آبان 1393 11
تقویم
مرداد 1402| ش | ی | د | س | چ | پ | ج |
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 21 | 22 | 23 | 24 | 25 | 26 | 27 |
| 28 | 29 | 30 | 31 |
جستجو
روشها و تکنیکهای انتگرال گیری-انتگرال گیری جانشانی
هر گاه در انتگرال با عبارتی مواجه شدیم که بصورت یک تابع مرکب و یک مشتق از پارامتر آن باشد ،می توان از این روش استفاده کرد .بصورت زیر:
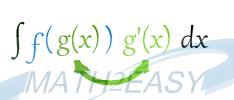
از عبارت بالا این را می فهمیم که در این روش تابع ![]() اینجا همان تابعی خواهد بود که باید از آن مشتق گرفته شود و اما تابع
اینجا همان تابعی خواهد بود که باید از آن مشتق گرفته شود و اما تابع ![]()
تابعی است که بصورت پارامتر تابع ![]() و علاوه براین مشتق تابع
و علاوه براین مشتق تابع ![]() هم وجود دارد پس آنچه باید تغییر پیدا کند همان تابع
هم وجود دارد پس آنچه باید تغییر پیدا کند همان تابع ![]() است .مثال پایین را ببینید :
است .مثال پایین را ببینید :
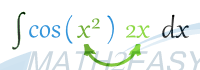
ببینید در مثال بالا تابع ![]() و تابع
و تابع ![]() برابر است با
برابر است با ![]() که مشتق آن برابر با
که مشتق آن برابر با ![]() می باشد
می باشد
پس الان فهمیدم که چگونه این توابع تفکیک می شوند و چه ارتباطی با هم دارند پس حالت کلی انتگرال بصورت زیر خواهد شد:
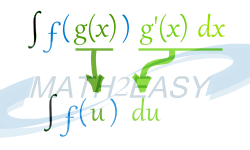
الان مثال بالا را با همان روش انتگرال جانشانی حل می کنیم تا مطلب را بهتر متوجه شویم :
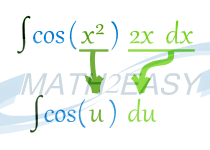
![]()
و چون ![]() پس خواهیم داشت که :
پس خواهیم داشت که :
![]()
اکنون که روش انتگرال گیری جانشانی و مفهوم آن را فرا گرفتیم برای فهم بهتر مطلب دو مثال را با هم حل می کنیم تا بهتر متوجه مطلب بشوید
مثال ۱: انتگرال ![]() را محاسبه کنید .
را محاسبه کنید .
ببینید نکته ای که در این انتگرال وجود دارد این است که شما همیشه همان حالت کلی را نخواهید داشت ، یعنی حتما تابع و مشتق آن مشخص نیست بلکه ممکن است نیاز باشد در عددی ضرب یا تقسیم و یا کمی تغییرات ایجاد کنید تا همان فرم روش جانشانی حاصل شود مثلا در این مثال باید انتگرال را بصورت زیر تبدیل کنیم :
![]()
پس با روش جانشانی بصورت زیر خواهد بود
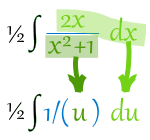
![]()
![]()
![]()
مثال ۲ : انتگرال ![]() را بدست آورید.
را بدست آورید.
![]()

![]()
![]()
![]()