
اخبار فناوری و شبکه
تازه های شبکه و IT
اخبار فناوری و شبکه
تازه های شبکه و ITنظرسنجی
نظرت رو راجع به مطالب وبلاگ بگو
جدیدترین یادداشتها
همه- جدیدترین آسیب پذیری های امنیتی 2023 در مایکروسافت
- ایجاد و پیکربندی DNS Zone در ویندوز سرور 2022
- سیستم مدیریت امنیت اطلاعات (ISMS) چیست؟
- آموزش کار با نرم افزار PyCharm
- ۱۰ عدد شگفتانگیز دنیای ریاضیات
- معرفی برترین سایت های آموزش زبان برنامه نویسی پایتون
- راهنمای جامع ارتقای رم لپ تاپ (+ آموزش تصویری)
- فروش حضوری محصولات مای نوکیا
- نقد و بررسی مشخصات سامسونگ galaxy J6 و galaxy J6 plus
- بهترین گوشی های موبایل پیشنهادی بر اساس قیمت (ویژه نوروز 1398)
بایگانی
- مرداد 1402 3
- فروردین 1398 16
- دی 1397 5
- آذر 1397 8
- تیر 1397 1
- خرداد 1397 10
- اردیبهشت 1397 5
- فروردین 1397 1
- آذر 1396 13
- خرداد 1396 5
- اردیبهشت 1396 4
- بهمن 1395 3
- اردیبهشت 1395 2
- بهمن 1394 17
- دی 1394 67
- آذر 1394 25
- آبان 1394 15
- مهر 1394 30
- شهریور 1394 16
- مرداد 1394 47
- تیر 1394 6
- خرداد 1394 12
- اردیبهشت 1394 115
- فروردین 1394 13
- اسفند 1393 5
- بهمن 1393 6
- دی 1393 2
- آبان 1393 11
تقویم
مرداد 1402| ش | ی | د | س | چ | پ | ج |
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 21 | 22 | 23 | 24 | 25 | 26 | 27 |
| 28 | 29 | 30 | 31 |
جستجو
آمار : 42005 بازدید
Powered by Blogsky
انتگرال گیری جزء به جزء به کمک تشکیل جدول
این حالت یکی از حالتهای خاص از روش جزء به جزء است که در معادلات دیفرانسیل کاربرد فراوانی دارد بگونه ای که اگر انتگرال ما بصورت ![]() باشد و در آن تابع
باشد و در آن تابع ![]() یک چند جمله ای باشد و تابع
یک چند جمله ای باشد و تابع ![]() یک تابع مثلثاتی مانند
یک تابع مثلثاتی مانند ![]() و یا
و یا ![]() یا
یا ![]() باشد بطوریکه در آن تابع
باشد بطوریکه در آن تابع ![]() پس از چند بار مشتق گیری صفر می شود و تابع
پس از چند بار مشتق گیری صفر می شود و تابع ![]() تابعی هست که به توان براحتی از آن انتگرال گرفت . نکته : این حالت برای زمانی استفاده می شود که نتوان انتگرال را بصورت جزء به جزء در یک مرحله محاسبه کرد .
تابعی هست که به توان براحتی از آن انتگرال گرفت . نکته : این حالت برای زمانی استفاده می شود که نتوان انتگرال را بصورت جزء به جزء در یک مرحله محاسبه کرد .
مراحل انجام روش جدولی
۱-یک جدول بصورت زیر رسم می کنیم که ستون اول آن مشتقات تابع ![]() تا زمانی که برابر صفر شود و ستون دوم آن انتگرالهای تابع
تا زمانی که برابر صفر شود و ستون دوم آن انتگرالهای تابع ![]()

۲-دو ستون جدول را بصورت مورب و یک در میان مثبت و منفی در هم ضرب می کنیم و سپس جملات را با هم جمع می کنیم تا جواب انتگرال بدست آید .
مثال ۱:
![]()
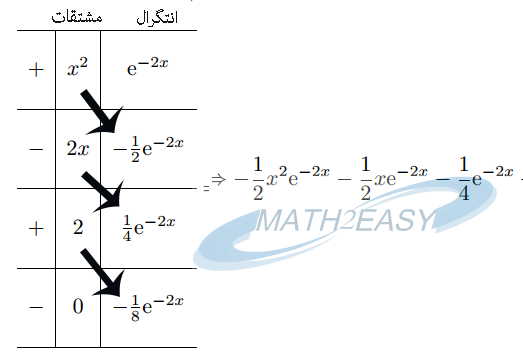
مثال ۲:
![]()
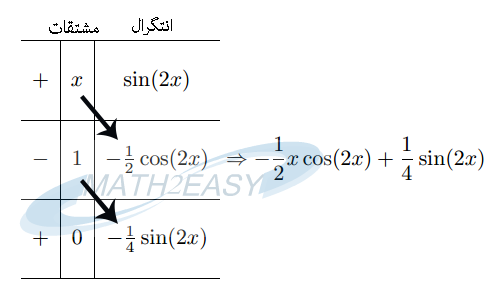
منبع:http://math2easy.com
Ali
شنبه 12 دی 1394 ساعت 16:30