الگوریتم پریم

الگوریتم پریم، الگوریتمی در نظریه گراف‌ها است که زیردرخت پوشای کمینه را برای یک گراف همبند وزن دار پیدا می‌کند یعنی زیرمجموعه‌ای از یال‌ها را در آن گراف می‌یابد که درختی را تشکیل می‌دهند که همه رئوس را شامل می‌شود در حالیکه مجموع وزن همه آن یال‌ها کمینه شده‌است. این الگوریتم در سال ۱۹۳۰ توسط ریاضیدانی به نام جارنیک داده شد وسپس در سال ۱۹۵۷ پریم، دانشمند علوم کامپیوتر آن را مستقل از جارنیک کشف کرد و در سال ۱۹۵۹ دایکسترا دوباره به آن دست یافت. ازاین رو این الگوریتم گاهی با نام الگوریتم DJP نیز شناخته می‌شود که برگرفته از اسامی دایکسترا، جارنیک و پریم است.

محتویات

• ۱ شرح الگوریتم
• ۲ هزینه زمانی
• ۳ مثال
• ۴ شبه کد الگوریتم پریم
• ۵ منابع
• ۶ پیوند به بیرون

شرح الگوریتم

این الگوریتم مرتب سازی درخت را که از یک یال شروع شده‌است، افزایش می‌دهد تاجائی که همه رئوس وارد درخت شوند.

این الگوریتم را به طور خلاصه می‌توان چنین شرح داد:

• ورودی: یک گراف همبند وزن دار با مجموعه رئوس V و یالهای E
• مقدار دهی اولیه: {V_new = {x که V_new مجموعه رئوس درخت پوشای کمینه در حالت آغازین را نشان می‌دهد و x یک راس دلخواه است (نقطه شروع) و
  {} = E_new که E_new بیانگر مجموعه یالهای این درخت است.
• حلقه زیر را تا وقتی که V_new = V تکرار کن:
  • یال (u,v) را با وزن کمینه انتخاب کن به طوری که u در V_new قرار داشته باشد ولی v عضوی از این مجموعه نباشد (اگر چند یال باوزن یکسان وجود دارند یکی را به دلخواه انتخاب کن)
  • راس v را به V_new و یال (u , v) رابه E_new اضافه کن.
• خروجی :V_new و E_new درخت پوشا. کمینه را توصیف می‌کنند.

نکته: الگوریتم پریم را به این صورت نیزمی توان بیان کرد:ابتدا گره ای به دلخواه انتخاب شود و سپس از بین یالهای متصل به آن یالی با کمترین وزن انتخاب می شود به گونه ای که حلقه ایجاد نشود.در هر مرحله یالی انتخاب می شود که حتماً یکی از دو سرآن جزو مسیر جواب بوده و وزن حداقل داشته باشد.پس درالگوریتم پریم دو محدودیت در هر مرحله داریم یکی آن که جنگل ایجاد نشود و دوم آنکه حلقه پدید نیاید.

از آنجا که درالگوریتم پریم درهرمرحله فاصله هر گره با گره های قبلی مقایسه می شود پس بدیهی است که ازمرتبه (n2)Ѳ می باشدکه n تعداد رئوس گراف است.

هزینه زمانی

یک پیاده سازی ساده، استفاده از نمایش گراف به صورت ماتریس مجاورت است که درآن به دنبال آرایه‌ای از وزنها باشیم و یال‌های با وزن کمینه را به مجموعه خود بیفزائیم. این روش (O(V^۲ زمان می‌برد. الگوریتم پریم بااستفاده از داده ساختار هیپ دودوئی ساده و نمایش فهرست مجاورت می‌تواند در زمان (O(E log V اجرا شود که در آن E تعداد یالها و V تعداد رئوس است. استفاده از مدل پیچیده تری به نام هیپ فیبوناچی باعث می‌شود این زمان تا حد (O(E + V log V کاهش یابد. سرعت این روش به خصوص زمانی آشکار می‌شود که در گراف رابطه (E = ω(V بین رئوس و یالها برقرار باشد.

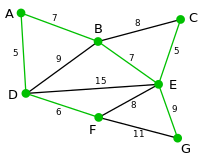
مثال

شکل	شرح
	این شکل گراف وزن دار اصلی را نشان می‌دهد. اعداد کنار هر یال بیانگر وزن آن یال هستند.
	راس D به طور دلخواه به عنوان نقطه ی شروع انتخاب شده‌است. رئوس A، B، E، F همگی با یالی به D متصل هستند. A نزدیک ترین راس به D است بنابراین همراه با یال AD برای درخت انتخاب می‌گردد.
	راس بعدی که انتخاب می‌شود باید نزدیک ترین راس به A یاD باشد. فاصله B از D برابر ۹ و فاصله آن از A برابر ۷ است. فواصل E وF نیز به ترتیب ۱۵ و ۶ می‌باشد. راس F کمترین فاصله را دارد بنابراین این راس و کمان DF را انتخاب می‌کنیم.
	الگوریتم مشابه بالا ادامه می‌یابد و راس B که فاصله اش از A برابر ۷ است انتخاب می‌شود.
	در این حالت انتخاب ما بین C، E، G می‌تواند صورت گیرد. فاصله C از B برابر ۸، فاصله E ازآن برابر ۷ و فاصله G از F نیز ۱۱ است. مشاهده می‌شود که E نزدیک ترین راس است پس آن را همراه با کمان BE انتخاب می‌کنیم.
	در اینجا تنها رئوس C و G باقی‌مانده‌اند. فاصله C از E برابر ۵ و فاصله G از آن ۹ است پس C انتخاب می‌شود و کمان CE نیز همزمان با آن وارد درخت می‌گردد.
	تنها راس باقی‌مانده G است که چون فاصله اش از E کمتر از فاصله اش تا F می‌باشد، یال EG را انتخاب می‌کنیم.
	در پایان همه رئوس انتخاب شده‌اند و درخت پوشای کمینه با رنگ سبز نشان داده شده‌است که وزنی برابر ۳۹ دارد.

شبه کد الگوریتم پریم

مسئله:یافتن کوچکترین درخت پوشا.

ورودی: عدد صحیح n>=2و یک گراف بدون جهت و وزن دار و پیوسته شامل n گره . گراف توسط یک آرایه دو بعدی w که سطر ها و ستونهایش ار 1 تا n شاخص دهی شده اند نشان داده می شود که در ان [w[i][j معرف وزن لبه بین گره i ام و گره j ام است .

خروجی:مجموعه ای از لبه ها F در یک درخت پوشای مینیمم برای گراف.

* void prim( int n,
*       const  number w[][],
*        set_of_edges  & F)
* {
*  index i, vnear;
*  number min ;
*  edge e;
*  index nearest[2..n];
*  number distance[2..n];
*  F = ∅ ;
*  for ( i = 2; i<=n;i++){
*    nearest[i] = 1 ;               
*    distance[i] = W[1][i];
*  }
*  repeat (n-1 times ){
*   min=∞;
*   for(i=2; i<=n; i++){
*     if(0≤ distance[i] <min ){
*       min = distance [i];
*       vnear = I  ;
*      }
*    e= edge connecting vertices indexed  by vnear and nearest[vnear  ];
*    add e to F ; 
*    distance[vnear]= -1
*    for ( i=2 ; i<= n ;i++)
*      if(W[i][vnear] <distance[i]){
*        distance[i] = w[i][vnear];
*        nearest[i] = vnear;
*       }
*     }
*   }

اگر در لحظه شروع {y={v1 باشد،لذا [nearest[i با 1 و [distance[i با وزن لبه بین v1 و vi مقدار دهی اولیه میشود.همانطوری که گره ها به Y اضافه میشوند،این دو ارایه برای ارجاع گره جدید در Y به نزدیکترین گره خارج از Y ، بهنگام (update)میشوند.برای معین کردن گره ای که باید به Y اضافه شوند ،در هر تکرار ،شاخصی که مقدار distance[i]1 ان مینیمم است را محاسبه می کنیم. این شاخص را vnear می نامیم. با مقداردهی [distance[vnear به1- ، گره با شاخص vnear به Y اضافه می گردد . الگوریتم بالا این روال را پیاده سازی میکند

if (y!=0)

{

   p+=e.weight;
     cout<<"("<<e.v1<<","<<e.v2<<") => W :"<<e.weight<<"\t";
      set[e.v1]=0;
      set[e.v2]=0;
        fe++;
        }
        else
              break;
  }
  return p;

 }

منبع: ویکی پدیا 

درخت های پو شای کمینه

فرض کنید طراح شهری می خواهد چند شهر معین را با جاده به هم وصل کند، به قسمی که مردم بتوانند از هر شهر به شهر دیگر بروند. اگر محدودیت بودجه ای در کار باشد ، ممکن است طراح بخواهد این کار را با حداقل  مقدار جاده کشی انجام دهد.

 

برای این مسئله دو الگوریتم حریصانه متفاوت : پریم و کروسکال بررسی می شود.

 

هر یک از این الگوریتم ها از یک ویژگی بهینه محلی استفاده می کند.

 

تضمینی وجود ندارد که یک الگوریتم حریصانه همواره حل بهینه بدهد، ثابت می شود که الگوریتم های کروسکال و پریم همواره درخت های پوشای کمینه را ایجاد می کنند.

 

پیچیدگی زمانی این دو الگوریتم: 

(T (n) = 2 ( n – 1) ( n – 1) Є θ ( n²

راهبرد عقبگرد

از تکنیک عقبگرد برای حل مسائلی استفاده می شود که در آن ها دنباله ای از اشیاء از یک مجموعه مشخص انتخاب می شود، به طوری که این دنباله ، ملا کی را در بر می گیرد.

یک مثال کلاسیک از عقبگرد، مسئله n وزیر است.

  

هدف از مسئله n وزیر ، چیدن n مهره وزیر در یک صفحه شطرنج است ، به طوری که هیچ دو وزیری یکدیگر را گارد ندهند. یعنی هیچ دو مهره ای نباید در یک سطر، ستون یا قطر یکسان باشند.

 

عقبگرد حالت اصلاح شده ی جست و جوی عمقی یک درخت است.

 

الگوریتم عقبگرد همانند جست و جوی عمقی است، با این تفاوت که فرزندان یک گره فقط هنگامی ملاقات می شوند که گره امید بخش باشدو در آن گره حلی وجود نداشته باشد.

تحلیل و بررسی الگوریتم کروسکال

عمل اصلی: یک دستور مقایسه.

اندازه ورودی : n ، تعداد رئوس و m  تعداد یال ها.

نکته: الگوریتم کروسکال همواره یک درخت پوشای کمینه تولید می کند.

 

اثبات : اثبات از طریق استقرا با شروع از مجموعه ای تهی از یال ها آغاز می شود.

 

void kruskal ( int n , int m,set _ of _ edges E,set _ of _edges & F )
index i , j ;
set _pointer p , q;
edge e ;
sort the m edges in E by weight in
nondecreasing order;
F = Ø ;
intitial (n) ;
while( number of edges in F is less than n-1){
e = edge with least weight not yet
considered ;
i , j = indices of vertices connected by e;
p = find (i) ;
q = find (i) ;
if (! equal ( p, q )) {
merge ( p , q ) ; add e to F ;
}

تحلیل الگوریتم پریم

void prim ( int n,const number W[ ] [ ],set_ of_edges & F )
{
index i , vnear;
number min;
edge e;
index nearest [2..n];
number distance [2..n];
F = Ø ;
for ( i = 2 ; i ≤ n ; i ++) {
narest [i] = 1 ;
distance [i] = W [1] [i] ;
}
repeat ( n-1 times ) {
min = ∞ ;
for ( i = 2 ; i < = n ; i ++)
if ( 0 ≤ distance [i] < min ) {
min = distance [i] ;
vnear = i ;
}
e = edge connecting vertices indexed by near and nearest [ vnear ] ;
add e to F ;
distance [ vnear ] = -1 ;
for ( i = 2 ; i ≤ n ; i ++)
if ( W[i] [ vnear ] < distance [i]) {
distance [i] = W [i] [ vnear ] ;
nearest [i] = vnear ;
}
}
}

مدیر تلگرامی که ماهی ۳۰ میلیون درآمد دارد

«رضا راد» یا «منصور قیامت» مدیر کانال «گیزمیز» یکی از محبوب ترین کانال های تلگرام است که حدود ۷۰۰ هزار مخاطب جمع کرده. اگر برایتان سوال است که زندگی یک مدیر تلگرام چطور می گذرد این مصاحبه را بخوانید. 

هیلو S؛ روتر مفهومی با مینی توسعه دهنده وای‌فای

هیلو S از بدنه استوانه ای شکل با طراحی ساده، زیبا و قابل حمل سود می برد. این روتر دارای سه توسعه دهنده برد وای فای دیسک شکل است.