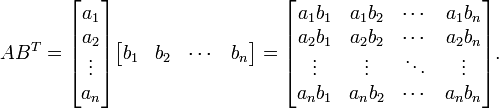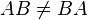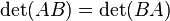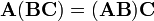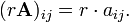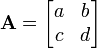اخبار فناوری و شبکه
تازه های شبکه و ITاخبار فناوری و شبکه
تازه های شبکه و ITضرب ماتریس
در جبر خطی ضرب ماتریس به عملیات ضرب یک ماتریس با یک کمیت نردهای یا یک ماتریس دیگر گفته میشود. در این مقاله سعی شده است تا نگاهی به انواع مختلف ضرب ماتریسی داشته باشیم.
|
|
ضرب معمولی ماتریسها رایجترین نوع ضرب در ماتریسهاست. این نوع ضرب تنها زمانی تعریف میشود که تعداد ستونهای ماتریس اول با تعداد سطرهای ماتریس دوم برابر باشد. حاصلضرب یک ماتریس m-در-n در یک ماتریس n-در-p یک ماتریس m-در-p است، به همین صورت اگر لیستی از ماتریسها برای ضرب را داشته باشیم که ابعاد مختلفی دارند (مانند m-در-n، n-در-p، p-در-q، q-در-r) بُعد ماتریس حاصلضرب از تعداد سطرهای اولین ماتریس و تعداد ستونهای آخرین ماتریس میآید (مثلا در لیست ذکر شده در بالا بعد ماتریس حاصلضرب m-در-r خواهد بود). توجه به این نکته نیز لازم است که ضرب ماتریسها خاصیت جابجایی ندارد.
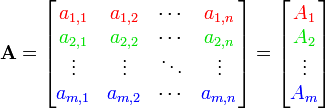
ضرب معمولی به این صورت تعریف میشود
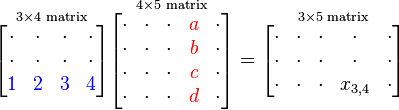
که در آن درایه 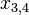 برابر است با :
برابر است با :
 .
.
برای به یادسپاری این موضوع میتوان ضرب معمولی را به این صورت القا کرد که سطر اول در ستون اول درایه اول و یا به صورت کلیتر سطر mم در ستون nم درایه mnم.
نمایش فرمولی
فرض کنید برای  و
و  در میدان
در میدان 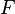 که
که 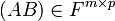 ، درایههای AB به صورت زیر بدست میآیند :
، درایههای AB به صورت زیر بدست میآیند :
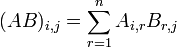
در اینجا i و j را اعداد طبیعی در نظر میگیریم که 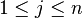 و
و  .
.
رابطه ضرب معمولی با ضرب داخلی و ضرب خارجی
ضرب داخلی و ضرب خارجی در حقیقت صورتهای خاص و سادهشدهای از ضرب معمولی ماتریسها هستند. ضرب دو بردار ستونی  و
و  به صورت
به صورت 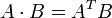 میباشد، دراینجا T نشانگر ترانهاده ماتریس است. به صورت صریحتر :
میباشد، دراینجا T نشانگر ترانهاده ماتریس است. به صورت صریحتر :
 .
.
ضرب خارجی به صورت 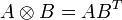 تعریف میشود که:
تعریف میشود که:
ضرب ماتریسها در پناه این دو عمل میتواند به صورت قطعهای مورد بحث قرار گیرد. برای شروع تجزیهی ماتریس به بردارهای سطری و بردارهای ستونی را بررسی میکنیم، در شکل زیر ماتریس A را به وسیله ماتریسی با بردارهای سطری و ماتریس B را به وسیله ماتریسی با بردارهای ستونی نمایش میدهیم :
که در اینجا  و
و 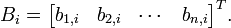 میباشند.
میباشند.
ضرب ماتریسی با این شیوه با توجه به تعاریف بالا به این صورت خواهد بود :
ویژگیها
- ضرب ماتریسی خاصیت جابجایی ندارد.
- اگر A و B دو ماتریس n-در-n باشند، دترمینان حاصلضرب به اولویت شرکت آنها در ضرب بستگی ندارد.
- اگر هر دو ماتریس قطری مربعی با ابعاد مشابه باشند، ضرب آنها جابجایی است.
- ضرب ماتریسی شرکتپذیر است:
- ضرب ماتریسی بروی جمع پخش میشود:

 .
.
- اگر ماتریس را تحت یک میدان (برای مثال میدانهای حقیقی یا مختلط) تعریف کنیم، آنگاه تحت هر اسکار از آن میدان جابجایی خواهد بود:
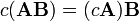


- در اینجا c یک اسکالر از میدان مربوطهاست.
ضرب اسکالر در ماتریس
ضرب اسکالر r در یک ماتریس A به این صورت تعریف میشود:
برای مثال اگر :
در نتیجه
ماتریس
ماتریس به یک آرایش منظم از اعداد گفته میشود. به طوری که میتوان گفت که هر ستون یا هر سطر یک ماتریس، یک بردار را تشکیل میدهد. در جبر خطی، میتوان اثبات کرد که هر نگاشت خطیِ، از فضای 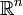 به فضای
به فضای 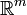 ، هم ارز (isomorph) با یک ماتریس
، هم ارز (isomorph) با یک ماتریس 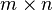 (m سطر و n ستون) می باشد. ماتریسها کاربردهای فراوانی در جبر خطی دارند. از جمله در انتقالهای خطی و در حل دستگاه معادلات خطی. ماتریسها میتوانند که با همدیگر جمع، از هم تفریق، در هم ضرب یا ... (با قوانین خودشان) بشوند.
(m سطر و n ستون) می باشد. ماتریسها کاربردهای فراوانی در جبر خطی دارند. از جمله در انتقالهای خطی و در حل دستگاه معادلات خطی. ماتریسها میتوانند که با همدیگر جمع، از هم تفریق، در هم ضرب یا ... (با قوانین خودشان) بشوند.
اگر دترمینان یک ماتریس مربعی نا صفر باشد، آنگاه آن ماتریس را ماتریس معکوسپذیر نامند.