اخبار فناوری و شبکه

اخبار فناوری و شبکه

تازه های شبکه و IT
اخبار فناوری و شبکه

اخبار فناوری و شبکه

تازه های شبکه و IT

تبدیلات لاپلاس

تبدیل لاپلاس (Laplace transform) یک تبدیل انتگرالی (integral transform) است که شاید نسبت به کارکرد تبدیل فوریه (Fourier transform) در حل مسائل فیزیکی در رتبه ی دوم قرار دارد. تبدیل لاپلاس به ویژه در حل معادلات دیفرانسیل معمولی (ordinary differential equations) که در تجزیه و تحلیل مدارهای الکترونیکی مطرح می شوند، دارای کاربرد فراوان است.

  تبدیل لاپلاس (یک طرفه)  L، که نبایستی آن را با مشتق لی (Lie derivative) که آن را هم معمولاْ با L نشان می دهند اشتباه گرفته شود، به صورت زیر تعریف می شود:

L_t[f(t)](s)=int_0^inftyf(t)e^(-st)dt,              

که  f(t) برای t>=0 تعریف می شود (Abramowitz and Stegun 1972). این تبدیل عموماً آن چیزی است که با عنوان تبدیل لاپلاس شناخته می شود، اگر چه یک تبدیل لاپلاس دوطرفه (bilateral Laplace transform) هم داریم که معمولاً به صورت زیر تعریف می شود:

L_t^((2))[f(t)](s)=int_(-infty)^inftyf(t)e^(-st)dt            

(Oppenheim et al. 1997).

تبدیل لاپلاس معکوس به انتگرال برومویچ (Bromwich integral) معروف است و گاهاً با عنوان انتگرال ملین-فوریه (Fourier-Mellin) نیز شناخته می شود.

جدول زیر، تعدادی از تبدیلات مهم لاپلاس یک طرفه را نشان می دهد:

f L_t[f(t)](s)

شرایط

1 1/s
t 1/(s^2)
t^n (n!)/(s^(n+1)) n in Z>=0
t^a (Gamma(a+1))/(s^(a+1)) R[a]>-1
e^(at) 1/(s-a)
cos(omegat) s/(s^2+omega^2) omega in R
sin(omegat) a/(s^2+omega^2) s>|I[omega]|
cosh(omegat) s/(s^2-omega^2) s>|R[omega]|
sinh(omegat) a/(s^2-omega^2) s>|I[omega]|
e^(at)sin(bt) b/((s-a)^2+b^2) s>a+|I[b]|
e^(at)cos(bt) (s-a)/((s-a)^2+b^2) b in R
delta(t-c) e^(-cs)
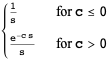H_c(t) {1/s for c<=0; (e^(-cs))/s for c>0
J_0(t) 1/(sqrt(s^2+1))
J_n(at) ((sqrt(s^2+a^2)-s)^n)/(a^nsqrt(s^2+a^2)) n in Z>=0

 در جدول بالا،  J_0(t) تابع بسل نوع اول (Bessel function of the first kind) مرتبه ی صفرام، delta(t) تابع دلتا (delta function) و H_c(t) تابع پله ی هوی ساید (Heaviside step function) هستند.

تبدیل لاپلاس خواص بسیار مهمی دارد. قضیه ی وجود تبدیل لاپلاس بیان می کند که اگر f(t) روی هر بازه ی متناهی در [0,infty) تکه ای پیوسته * باشد و برای همه ی t in [0,infty) در

|f(t)|<=Me^(at)                 

صدق کند، آن گاه  L_t[f(t)](s) برای همه ی s>a موجود است. تبدیل لاپلاس یکتا (unique) است، به این معنی که با داشتن دو تابع  F_1(t) و  F_2(t) با تبدیل یکسان، داریم:

L_t[F_1(t)](s)=L_t[F_2(t)](s)=f(s),        

آن گاه قضیه ی لرچ (Lerch's theorem) تایید می کند که انتگرال

int_0^aN(t)dt=0           

برای همه ی a>0 برای یک تابع صفر (پوچ - null function) با معادله ی

N(t)=F_1(t)-F_2(t).                    

صفر می شود. تبدیل لاپلاس خطی است، زیرا

int_0^infty[af(t)+bg(t)]e^(-st)dt   =   L_t[af(t)+bg(t)]         

aint_0^inftyfe^(-st)dt+bint_0^inftyge^(-st)dt   =                                       

aL_t[f(t)]+bL_t[g(t)].    =                                       

تبدیل لاپلاس کانولوشن (convolution) به صورت زیر تعریف می شود:

L_t[f(t)*g(t)]=L_t[f(t)]L_t[g(t)] L_t^(-1)[FG]=L_t^(-1)[F]*L_t^(-1)[G].


جال مشتق گیری را در نظر می گیریم. فرض کنیم  f(t)،  n-1 بار در [0,infty) مشتق پذیر باشد. اگر  |f(t)|<=Me^(at)، آنگاه

L_t[f^((n))(t)](s)=s^nL_t[f(t)]-s^(n-1)f(0)-s^(n-2)f^'(0)-...-f^((n-1))(0).         

این را میتوان به کمک انتگرال جزء به جزء آشکار ساخت:

lim_(a->infty)int_0^ae^(-st)f^'(t)dt   =   L_t[f^'(t)](s)         

lim_(a->infty){[e^(-st)f(t)]_0^a+sint_0^ae^(-st)f(t)dt}   =                              

lim_(a->infty)[e^(-sa)f(a)-f(0)+sint_0^ae^(-st)f(t)dt]   =                              

sL_t[f(t)]-f(0).  =                              

ادامه ی این روش به مشتقات مرتبه ی بالاتر نتیجه می دهد:

L_t[f^('')(t)](s)=s^2L_t[f(t)](s)-sf(0)-f^'(0).            

ار این خاصیت تبدیل لاپلاس می توان در تبدیل معادلات دیفرانسیل به معادلاتی جبری استفاده کرد که به حساب هوی ساید (Heaviside calculus) معروف است. آنگاه با انجام تبدیل وارون می توان به پاسخ دست یافت. به عنوان مثال، بکار بردن تبدیل لاپلاس برای معادله ی دیفرانسیلی

f^('')(t)+a_1f^'(t)+a_0f(t)=0            

خواهیم داشت:

{s^2L_t[f(t)](s)-sf(0)-f^'(0)}+a_1{sL_t[f(t)](s)-f(0)}+a_0L_t[f(t)](s)=0        

L_t[f(t)](s)(s^2+a_1s+a_0)-sf(0)-f^'(0)-a_1f(0)=0,        

که آخری را می توان به شکل زیر بازنویسی کرد:

L_t[f(t)](s)=(sf(0)+f^'(0)+a_1f(0))/(s^2+a_1s+a_0).        

اگر تبدیل وارون لاپلاس را بتوان بر این معادله اعمال کرد، آن گاه معادله ی دیفرانسیل اصلی حل می شود.

تبدیل لاپلاس در چند خاصیت مهم صدق می کند. نمایی کردن (exponentiation) را در نظر بگیرید. اگر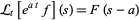 برا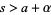ی  (یعنی 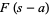 تبدیل لاپلاس f باشد)، آن گاه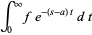 برای s>a+alpha صحیح است. زیرا

int_0^inftyfe^(-(s-a)t)dt   =       F(s-a)           

int_0^infty[f(t)e^(at)]e^(-st)dt    =                              

L_t[e^(at)f(t)](s).   =                              

همچنین تبدیل لاپلاس خواص زیبایی را برای انتگرال های توابع دارد. اگر  f(t) تکه ای پیوسته (piecewise continuous) بوده و |f(t)|<=Me^(at)، در آن صورت

L_t[int_0^tf(t^')dt^']=1/sL_t[f(t)](s).

Ali دوشنبه 27 مهر 1394 ساعت 11:41
نظرات 0 + ارسال نظر
امکان ثبت نظر جدید برای این مطلب وجود ندارد.