تکنیکهای انتگرال گیری-انتگرال گیری به روش جزء به جزء

انتگرال با روش جزء به جزء یکی از روشهای جالب انتگرال گیری است .شاید بشه گفت ممکن است پس از امتحان روشهای دیگر ،درنهایت شما این روش را انتخاب خواهید کرد .ایده این روش بسیار ساده است و از روش ضرب توابع و محاسبه مشتق ضرب توابع پیروی می کند .

ما از بخش مشتق می دانیم که مشتق حاصلضرب دوتابع بصورت زیر است:

$(f(x).g(x))' = f(x)'.g(x) + f(x).g'(x)$

خوب اکنون ما از رابطه بالا انتگرال می گیریم :

$\int (f(x).g(x))'dx = \int f(x)'.g(x)dx + \int f(x).g'(x)dx$

از طرفی دیگر می دانیم که انتگرال گیری از یک مشتق برابر می شود با خود آن تابع یعنی :

$\int (f(x).g(x))' = f(x).g(x)$

پس رابطه بالای ما بصورت زیر خواهد شد:

$f(x).g(x) = \int f(x)'.g(x)dx + \int f(x).g'(x)dx$

که در نهایت بصورت زیر می نویسیم :

$\int f(x).g'(x)dx=f(x).g(x)- \int f(x)'.g(x)dx$

اکنون از همین فرمول بالا هم می توان برای محاسبه انتگرال استفاده کرد اما ما اینجا می خواهیم فرمول عمومی انتگرال جزء به جزء را بدست آوریم لذا اگر در تابع فوق جایگزینهای زیر را قرار دهیم :

$\left\{ \begin{array}{l} u = f(x) \\ du = f'(x)dx \\ \end{array} \right\}\left\{ \begin{array}{l} v = g(x) \\ dv = g'(x)dx \\ \end{array} \right\}$

آنگاه فرمول کلی انتگرال جزء به جزء ما بصورت زیر بدست می آید :

$\int u dv = uv - \int {vdu}$

معمولا این روش برای محاسبه انتگراهای ضرب دوتابع بکار می رود ،دو تابعی که هر کدام از جنس مختلفی می باشد ،مثلا ضرب یک چند جمله ای در یک تابع مثلثاتی و …چند نمونه از این حالتها را در زیر مشاهده کنید:

$\begin{array}{l} \int {x\sin xdx} \\ \int {x{e^x}} dx \\ \int {{e^{2x}}} \cos xdx \\ \end{array}$

این روش که مبتنی بر ضرب دوتابع است و ما با استفاده از ((قاعده مشتقگیری ضرب دوتابع )) انتگرال را بدست می آوریم

یکی از مهمترین خصوصیات این روش تبدیل انتگرالهای پیچیده به انتگرالهای ساده تر است.که می توانیم آن را با استفاده از فرمول بالا حل کنیم . اکنون سوالی مطرح می شود که کدام یک را تابع $u$ و کدام را تابع $v$ در نظر بگیریم ، برای جواب باید گفت که مبنای ما بصورت زیر است

۱- $u$ را برابر تابعی قرار می دهیم که براحتی قابلیت مشتق گیری و دیفرانسیل گیری داشته باشد

۲- $dv$ برابر است با تابعی که به توان راحتتر از آن انتگرال گرفت

۳-محاسبه انتگرال $\int vdu$ آسان تر است از محاسبه $\int udv$

مثال ۱:انتگرال زیر را حساب کنید

$\int x\sin2xdx$

ببینید برای حل انتگرال ها شما با این سوال مواجه می شوید که کدام تابع فوق را v و کدام را معادل u قرار دهیم ما اینجا طبق قاعده بالا u را معمولا برابر تابعی قرار می دهیم که dx ما براحتی با du جایگزین شود و محاسبه انتگرال $dv$ برای ما هم ساده تر بشود . پس در واقع به انتخاب شما و ابتکار شما نیاز دارد که تشخیص دهید چگونه توابع را جایگزین کنید.

اکنون سعی می کنیم قدم به قدم مثال بالا را حل کنیم :

قدم اول : تشخیص تابع u و تابع دیگر به همراه dx که برابر با dv خواهد بود .

$u=x \Rightarrow du=dx$

$dv = \sin 2xdx$

قدم دوم : از u دیفرانسیل می گیریم تا du بدست آید و از dv انتگرال می گیریم تا v بدست آوریم .

$u=x \Rightarrow du=dx$

$dv = \sin 2xdx \Rightarrow v = \int {\sin 2xdx} = - \frac{1}{2} \cos 2x$

قدم سوم : عبارتهای فوق را در فرمول انتگرال گیری جزء به جزء قرار می دهیم و حاصل انتگرال را بدست می آوریم :

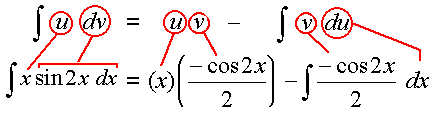
انتگرال جزء به جزء

$=\frac{-x\cos 2x}{2}+\frac{1}{2}\int \cos 2xdx \\=\frac{-x\cos 2x}{2}+\frac{1}{2}\left ( \frac{sin2x}{2} \right )+k \\=\frac{-x\cos 2x}{2}+\left ( \frac{sin2x}{4} \right )+k$

http://math2easy.com:منبع

Ali شنبه 12 دی 1394 ساعت 16:28

ش	ی	د	س	چ	پ	ج
	1	2	3	4	5	6
7	8	9	10	11	12	13
14	15	16	17	18	19	20
21	22	23	24	25	26	27
28	29	30	31

اخبار فناوری و شبکه

اخبار فناوری و شبکه

نظرسنجی

تقویم